Can Paradoxes Lead to Consistency?

A paradoxical statement states that, if it is what it states, then it is not what it states. For instance, "I am a liar." If I am a liar, then I lied in stating this sentence and then I am not a liar. If I am not a liar, then I am saying the truth and the sentence stating that I am a liar is true. However, if it is true, then I cannot say the truth, etc.

The Holophanic Loop Logic distinguishes between first-degree and second-degree paradoxes. Within the ‘if-then' logical structure of a first-degree paradox, the ‘then' is the exact opposite of the ‘if'. The inner structure of a first-degree paradox could be characterized by the following:

1. 1. it is contained within one system, one closed loop, referring back to itself (self-referential)
   2. it establishes sameness
   3. the meaning of a paradox relates to its own structure and is not the symbol of some other idea
   4. it is one statement or idea that leads to an inverse idea of equal weight (I would rather call it inverse than opposite)
   5. the inverse ideas mutually exclude each other, yet when focused upon, one leads to the other, which then leads back to the first one and so on
   6. the dynamic of the paradox negates its own definition, which gains expression as one idea leading to its inverse counterpart
   7. this leading of one idea to its inverse counterpart is dynamic since both cannot coexist simultaneously within the same system
   8. this dynamic activity within one system is an unbroken line, and hence, the paradox is generative of an inner motion, something like a Möbius strip - one needs to make two circles to get back to the same point, one on the outer (convex) surface and one on the inner (concave) surface in an unbroken line
   9. one of the inverse ideas that leads to the other is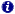 "Significance", whereas the other represents 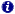"Structure"

Holophany relates to paradoxes within which the inverse parts are not of equal value (they are asymmetric), as second-degree paradoxes. Within the ‘if-then' logical structure of a second-degree paradox, the ‘then' is the almost opposite of the ‘if'. The motion between these inverse parts is considered the motive force of creativity. An example of a second-degree paradox could be: "Can the omnipotent God make a stone so heavy that he can't lift it?" Of course he can, since God is omnipotent, he can do anything he wishes. But if he can't lift the stone, then he is not the omnipotent God, and of course, then he cannot create such a stone. If there is no such stone that God cannot lift, then God is omnipotent and then he can create such a stone that even he himself cannot lift, etc. Here is the Möbius process again. However, a second-degree paradox diverges from a first-degree paradox because:

1. 10. its inverse parts are not of equal weight
   11. its inner motion is generative of higher dimensionality
   12. it is self-transcendent while maintaining its self-referential framework (not one closed loop)
   13. its creative aspect is due to repetitious self-similarity wherein each outcome is a bit different than the others (i.e., more contracted)
   14. its creative aspect is due to feedback
   15. it generates higher and higher levels of complexity

According to this, a possible solution to the above paradox could be, as follows: on the one hand, God creates a stone that no one, not even he, can lift, and then creates a self that can lift that stone; in turn, that self can create a stone that this self cannot lift, but he can create a self that can lift the stone, which can create a stone that he himself cannot lift, etc. On the other hand, he cannot create such a stone if he cannot create infinitely recursive selves that alternately can and cannot lift the stone.

Structure versus Significance

The stabilized entity within the borders of the definition, i.e. what has been defined, is significance. The process of definition, the dynamics that bring about stabilization, is structure. The claim of Holophany is that the variety that we can perceive is significance whereas the structure of any and all significance is the isomorphous logical structure, the process of definition. Whereas what has been considered to be truth or fallacy always relates to significance, structure relates to the method that defines something to be true or false.

Consistency to be Consistent, Must Include the Indefinite

The sheer structure of any definition implies that there is something beyond the borders of the defined (see also How is there Something from Nothing?). What we know about this something or somethings (everything else beyond the borders of the defined) is that these are not our defined object. When we focus on what is being defined, whatever is beyond the border of the definition is indefinite. The necessary implication that the indefinite must be beyond the borders is, however, definite. What is implied is indefinite, but that it is implied is definite. Another way of saying this is, if ‘a' has been defined, then ‘a' is definite. However, for ‘a' to have meaning, the definition has to imply the beyond, the indefinite, the ‘not-a.' Thus, ‘a' cannot be definite unless it has meaning, which indicates that if ‘a' is ‘a,' then ‘not-a' (although implicitly implied) is also part of ‘a' - which is an inconsistency.

Viewing only the defined ‘a' is a truncated view, incomplete but consistent. If we look at the whole process of definition that includes the indefinite, we discover the inconsistency within the definition. That is why paradoxes are so basic to Holophany. Perception and what is being perceived include the tools of definition, which render it a loop. The contradiction between two significances is inconsistency, whereas the contradiction between structure and significance that lead to each other is a paradox.

When the meaning of something is dependent on the indefinite, on what our defined object is not, then this indefinite must necessarily be included in the process of definition. So including the tools of the definition yields both definite, indefinite and also inconsistent elements, which is the only logical way for the process of definition to be consistent. This logical implication that perception of meaning is only possible if and only if the indefinite is included within the perception is the reason why the dream of a consistent and complete axiomatic system with only well defined (explicit) empty signs had to fail (see The Loop Logic). When Gödel proved that arithmetic was incomplete by showing that there were propositions that could neither be proved nor disproved from the system's axioms alone, he showed that these undecidable propositions meant that the system was inconsistent because it could not be decided from the axioms of the system whether they were ‘a' or ‘not-a.' Of course, undecidable means indefinite. This closed the door on the 19th century dream of a complete and consistent axiomatic system. Nevertheless, it opened the door to something else.

In spite of the fact that logic is the fundament of algorithms and computer science, it had neither the aspiration nor the ability to be connected to the real world precisely because its propositions were so anemic regarding meaning. In the effort to exclude any hint of the indefinite, logical inference was confined to a binary type of world of true and false and lacking any correlation with life and experiencing. However, including the indefinite in the process of definition not only makes the Loop Logic the fundament of existence, but determines the necessity of existence.[1] When existence is relations, and relating is the act of perceiving, and perceiving is the process of definition, then existence is the overall lawfulness, the isomorphous lawfulness of the process of definition. What is being perceived, what is being stabilized, which significance is brought to the foreground from the amorphous background of the indefinite, depends on the non-linear rules of complex interactions. Thus the Loop Logic emphasizes the creation of essents rather than their interactions.

Attempting to define the indefinite creates a paradox, which in turn creates something defined and also the indefinite; no matter how much the indefinite will be defined, it will stay indefinite, but at the same time, the act of trying to define the indefinite will yield a manifold of definitions. A paradox produces the distinction between the structure and significance of the paradox. (For example, "I am a liar" is significance, it is the definition of what I am. Claiming that "I cannot truthfully state that I am a liar" is stated about the definition, and in itself, is not the definition; this meta-statement is structure. Another example: 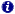"Indefinite" is structure, but when I try to say, "indefinite means that something cannot be bounded to have meaning," which could be the definition of "indefinite," then this definition is significance. "Indefinite" is a paradox because the meaning of the significance - namely, that it cannot be defined is in contradiction with the structure that defined it.) The dynamic implied by the paradox creates the process of definition, which closes the loop. Simplified, the loop is between structure and significance, which perpetuates both. Or we could start with significance. To have significance with meaning, anything must have structure, it has to be defined, which act also creates the indefinite. When we try to sharpen our definition to include the indefinite, we reach the paradox. No matter where we start, we will have the loop that does not necessitate a beginning, which can start anywhere with an assumption and then derive this assumption retromorphously from the process of the loop. Although a closed loop, this logic creates/is the isomorphous structure of existence.

[1] The proof can be found in Holophany, the Loop of Creation.